Ball & Beam Control - Modeling

VIA[CTM]

Modeling the Ball and Beam Experiment

Problem Setup

A ball is placed on a beam, see figure below, where it is allowed to roll with 1 degree of freedom along the length of the beam. A lever arm is attached to the beam at one end and a servo gear at the other. As the servo gear turns by an angle theta, the lever changes the angle of the beam by alpha. When the angle is changed from the vertical position, gravity causes the ball to roll along the beam. A controller will be designed for this system so that the ball's position can be manipulated.

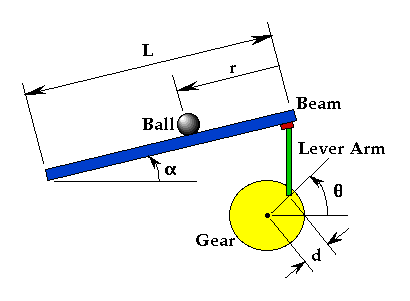
For this problem, we will assume that the ball rolls without slipping and friction between the beam and ball is negligible. The constants and variables for this example are defined as follows:

• M.........mass of the ball  0.11 kg 
• R.........radius of the ball  0.015 m 
• d.........lever arm offset  0.03 m 
• g.........gravitational acceleration  9.8 m/s^2 
• L.........length of the beam  1.0 m 
• J.........ball's moment of inertia  9.99e-6 kgm^2 
• r.........ball position coordinate  
• alpha.....beam angle coordinate  
• theta.....servo gear angle  
  

The design criteria for this problem are:

• Settling time less than 3 seconds
• Overshoot less than 5%

System Equations

The Lagrangian equation of motion for the ball is given by the following:

Linearization of this equation about the beam angle, alpha = 0, gives us the following linear approximation of the system:

The equation which relates the beam angle to the angle of the gear can be approximated as linear by the equation below:

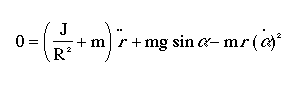
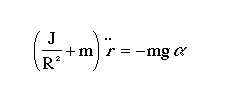
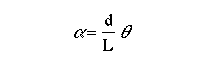
Substituting this into the previous equation, we get:

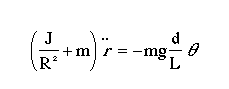
1. Transfer Function
Taking the Laplace transform of the equation above, the following equation is found:

NOTE: When taking the Laplace transform to find the transfer function initial conditions are assumed to be zero.

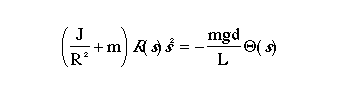
Rearranging we find the transfer function from the gear angle (theta(s)) to the ball position (R(s)).

It should be noted that the above plant transfer function is a double integrator. As such it is marginally stable and will provide a challenging control problem.

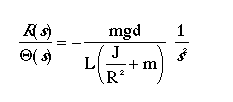
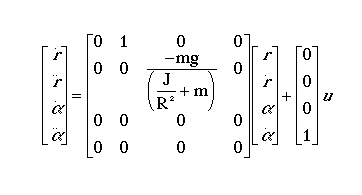
2. State-Space
The linearized system equations can also be represented in state-space form. This can be done by selecting the ball's position (r) and velocity (rdot) as the state variables and the gear angle (theta) as the input. The state-space representation is shown below:

However, for our state-space example we will be using a slightly different model. The same equation for the ball still applies but instead of controlling the position through the gear angle, theta, we will control alpha-doubledot. This is essentially controlling the torque of the beam. Below is the representation of this system:

Note: For this system the gear and lever arm would not be used, instead a motor at the center of the beam will apply torque to the beam, to control the ball's position.

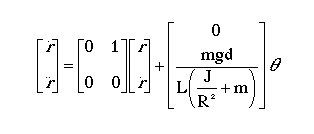
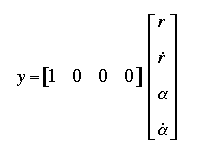
Matlab Representation and Open-Loop Response

1. Transfer Function
The transfer function found from the Laplace transform can be implemented in Matlab by inputting the numerator and denominator as vectors. To do this we must create an m-file and copy the following text into it:

.......m = 0.111;
.......R = 0.015;
.......g = -9.8;
.......L = 1.0;
.......d = 0.03;
.......J = 9.99e-6;

.......K = (m*g*d)/(L*(J/R^2+m));   %simplifies input

.......num = [-K];
.......den = [1 0 0];
.......printsys(num,den)

Your output should be:

.......num/den =   0.21 / ( s^2 )

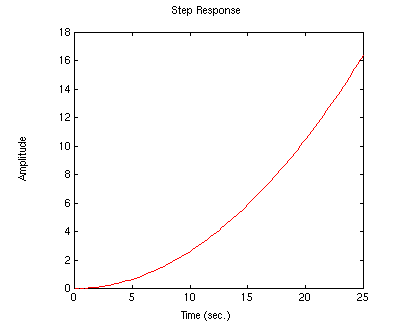
Now, we would like to observe the ball's response to a step input of 0.25 m. To do this you will need to add the following line to your m-file:

.......step(0.25*num,den)

NOTE: Matlab commands from the control system toolbox are highlighted in red.

You should see the following plot showing the balls position as a function of time:

From this plot it is clear that the system is unstable in open-loop causing the ball to roll right off the end of the beam. Therefore, some method of controlling the ball's position in this system is required. Three examples of controller design are listed below for the transfer function problem. You may select from PID, Root Locus, and Frequency Response.

2. State-Space
The state-space equations can be represented in Matlab with the following commands (these equations are for the torque control model).

.......m = 0.111;
.......R = 0.015;
.......g = -9.8;
.......J = 9.99e-6;

.......H = -m*g/(J/(R^2)+m);
  
.......A=[0 1 0 0
.......   0 0 H 0
.......   0 0 0 1
.......   0 0 0 0];
.......B=[0;0;0;1];
.......C=[1 0 0 0];
.......D=[0];

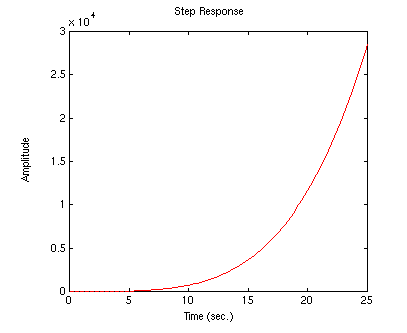
The step response to a 0.25m desired position can be viewed by running the command below:

.......step(A,B*.25,C,D)

Your output should look like the following:

Like the plot for the transfer function this plot shows that the system is unstable and the ball will roll right off the end of the beam. Therefore, we will require some method of controlling the ball's position in this system. The State-Space example below shows how to implement a controller for this type of system.